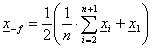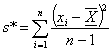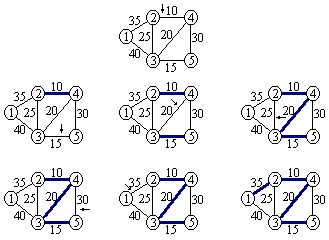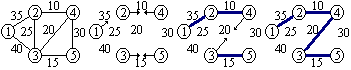Zárthelyi feladatok, és megoldásaik
1.
Zárthelyi
feladat: 2002.02.18 12.00 óra
A csoport:
Egész (típusú) tömbben a hárommal osztható elemek átlagának
meghatározása. (Amennyiben nincs ilyen elem a tömbben, akkor 0-t adjon vissza
a függvény. Megoldásra szánt idő: 2 perc)
Megoldás: ZH01A.Cpp
B csoport: Valós
(típusú) tömbben a pozitív elemek közül a legkisebb érték meghatározása.
(Amennyiben nincs pozitív elem a tömbben, akkor a függvény -1-el térjen
vissza. Megoldásra szánt idő: 3 perc)
Megoldás: ZH01B.Cpp
2.
Zárthelyi
feladat: 2002.02.25 12.00 óra
A
csoport: Valós (típusú) tömb
elemeinek varianciájának meghatározása (Megoldásra szánt idő: 3 perc)
Megoldás:
ZH02A.Cpp
B
csoport: Egész (típusú) tömb
elemeinek egymáshoz képesti távolságának meghatározása (Megoldásra szánt
idő: 2 perc.)
Megoldás:
ZH02B.Cpp
3. Zárthelyi feladat: 2002.03.04 12.00 óra
A csoport: Rendezzen növekvő sorrendben egy egész (típusú) tömböt a maximum kiválasztás módszerével. (Megoldásra szánt idő: 3 perc.)
Megoldás: ZH03A.Cpp
B csoport: Rendezzen
csökkenő sorrendben egy valós (típusú) tömböt a buborék rendezés módszerével.
(Megoldásra szánt idő: 2 perc.)
Megoldás:
ZH03B.Cpp
4.
Zárthelyi feladat: 2002.03.11 12.00 óra
A
csoport: Készítsen egy olyan
logikai függvényt, mely egy paraméterül kapott pozitív egész számról eldönti,
hogy prímszám vagy sem. (Megoldásra szánt idő: 2 perc.)
Megoldás: ZH04A.Cpp
B
csoport: Valós típusú tömb átlagtól
való abszolút eltérésének meghatározása (Megoldásra szánt idő: 3
perc.)
Megoldás:
ZH04B.Cpp
5.
Zárthelyi feladat: 2002.03.18 12.00 óra
A
csoport: Kérje be egy adott
intervallumba eső valós tömb értékeit. Írja le a teljes programot. (Megoldásra
szánt idő: 8 perc.)
Megoldás:
ZH05A.Cpp
B
csoport: Verem megvalósítása
dinamikusan láncolt kétirányú listával. (Megoldásra szánt idő: 7 perc.)
Megoldás: ZH05B.Cpp
6.
Zárthelyi feladat: 2002.03.25 12.00 óra
A csoport: FIFO megvalósítása
dinamikusan láncolt kétirányú listával. (Megoldásra szánt idő: 15 perc.)
Megoldás:
ZH06A.Cpp
B csoport: Kétféle
területszámoló eljárás azonos őssel és módosított virtuális metódussal.
Az egyik metódus egy kör, még a másik egy négyzet területét számítja
ki. Írja le a teljes programot. (Megoldásra szánt idő: 16 perc.)
Megoldás:
ZH06B.Cpp
7.
Zárthelyi feladat: 2002.04.08 12.00 óra
A csoport: Rendezzen
csökkenő sorrendbe egy valós tömböt a bináris keresőfa segítségével. Írja le a teljes programot. (Megoldásra szánt idő: 16 perc.)
Megoldás:
ZH07A.Cpp
B csoport: Írjon olyan függvényt, mely egy valós tömb második
legnagyobb elemét adja vissza. Írja le a teljes programot. (Megoldásra szánt
idő: 15 perc.)
Megoldás:
ZH07B.Cpp
8.
Zárthelyi feladat: 2002.04.15 12.00 óra
A csoport: Készítse el a string osztály != összehasonlító operátorát.
(Megoldásra szánt idő: 3 perc.)
Megoldás:
ZH08A.Cpp
B
csoport: Készítse el a string osztály <= összehasonlító operátorát.
(Megoldásra szánt idő: 4 perc.)
Megoldás:
ZH08B.Cpp
9.
Zárthelyi
feladat: 2001.04.22 12.00 óra
A csoport: Készítse el a string osztály két konverziós
konstruktorát, melyek közül az egyik konstruktor paramétere egy karakter, a
másik konstruktor paramétere egy char* karakter tömb. (Megoldásra szánt idő:
3 perc.)
B
csoport: Készítse el a string osztály = operátor felüldefiniálásait.
(Megoldásra szánt idő: 4 perc.)
Megoldás:
ZH09.Cpp
10.
Zárthelyi
feladat: 2001.04.29 12.00 óra
A csoport: Készítse el a string osztály [] operátor felüldefiniálását.
(Megoldásra szánt idő: 2 perc.)
B csoport: Készítse el a string osztály + operátor felüldefiniálását.
(Megoldásra szánt idő: 3 perc.)
Megoldás:
ZH10.Cpp
Gyakorlati órákon tárgyalt feladatok, és
megoldásaik
1. Gyakorlat: A C++ nyelvi elemeinek gyakorlása feladatokkal.
- Valós (dinamikusan lefoglalt) tömb adatainak bekérése, összeg/átlag
meghatározása.
Összeg:
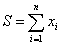 ,Átlag:
,Átlag:
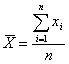 .
.
- Helyzeti mutatók, középértékek, szóródási mutatók meghatározása:
a.) Harmonikus átlag:
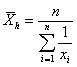
b.) Mértani átlag:
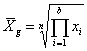
c.) Négyzetes átlag:
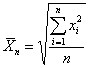
d.) r-ed rendű momentum:
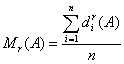 , ahol
, ahol
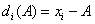
e.) Terjedelem:
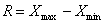
f.) Átlagos (abszolút) eltérés:
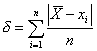
g.) Variancia:
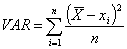
h.) Szórás:
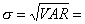
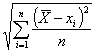
i.) Realtív szórás:
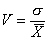
j.) Átlagos
(abszolút) különbség:
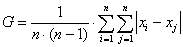
A gyakorlati feladat megoldása:
Orai01.Cpp
1. Gyakorlat (Házi feladat): További helyzeti és
alakmutatók.
1., Helyzeti mutatók: Módusz, medián, kvantilisek (kvintilisek,
kvartilisek, decilisek, percentilisek) meghatározása
2., Alak mutatók: Ferdeségi mutatók: Pearson, F-mutatók, a3-mutató.
Csúcsossági mutatók K-mutató, a4-mutató
Megjegyzés:
ahhoz, hogy a kvantililseket ki tudjuk számolni, vagy osztályokat kell képezni,
vagy rendezni kell az elemeket.
A házi feladat megoldása:
HF01.Cpp
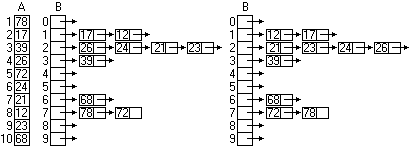
2. Gyakorlat: A C++ nyelvi elemeinek gyakorlása feladatokkal. II
1., Egész típusú (dinamikusan lefoglalt) tömb véletlen adatokkal való feltöltése, átmásolása egy másik tömbbe. A tömbök rendezése
minimum-kiválasztásos, és buborékrendezés segítségével. A futásidők összehasonlítása.
2., A sin(x2)
a és b közötti határozott integráljának meghatározása az alábbi
numerikus integrál közelítő módszerekkel. Készítsen olyan függvényt,
amely fokból radiánba, radiánból fokba számít.
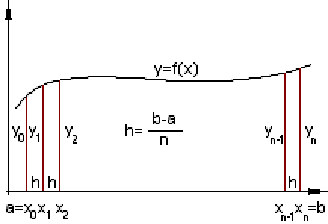
§
Téglalap formula: h(y0+y1+y2+..+yn-1),
vagy h(y1+y2+..+yn-1+yn)
§
Trapéz formula: h(y0/2+ y1+y2+..+yn-1+
yn/2)
§
Simpson formula: h(y0+ 4y1+2y2+4y3+..+2yn-2+4yn-1+
yn)/3 (ha n=2k)
Orai02-1.Cpp, Orai02-2.Cpp
2. Gyakorlat (Házi feladat): Tetszőleges függvény határozott
integráljának meghatározása a három integrálközelítő módszer segítségével.
A függvény értelmezését végezze el a lengyel formula segítségével!
Integral.Cpp, Integral.Doc
(Bocska István)
3-4. Gyakorlat: Feladatok osztályokkal.
- Készítse el a következő osztálydefiníciót, és hozza létre az osztály
egy statikus példányát.
CString;
Adattagok:
Buffer //Ez tartalmazza a stringet.
WordCount //A stringben szereplő szavak számát tartalmazza.
Length //A string hosszát tartalmazza.
Fügvénytagok: (saját függvények)
SetSeparator //Az elválasztó jelet állítja be.
SetCount //A szavak számát állítja be.
(nyilvános függvények)
SetString //Új stringet definiál.
GetString //Visszaadja a jelenleg tárolt stringet.
GetWordCount //A szavak számát adja vissza.
GetLength //A string hosszát adja vissza.
Készítsen két konstruktort. Egy alapértelmezettet, mely a Buffer-nek
egy üres stringet ad át, és egy olyat, melynek át lehet adni egy
stringet, valamint készítsen destruktort is.
- Készítsen egy CVertex osztályt, mely tartalmazza, a valós típusú
vektort, a szükséges bekérő, módosító, lekérdező függvényeket. Készítsen
olyan CVertexes objektumot, melynek VCount db. vektortagja van, tartalmazza
az osztály olyan függvényt, mely visszaadja a vektorok összegét, és
skaláris szorzatát.
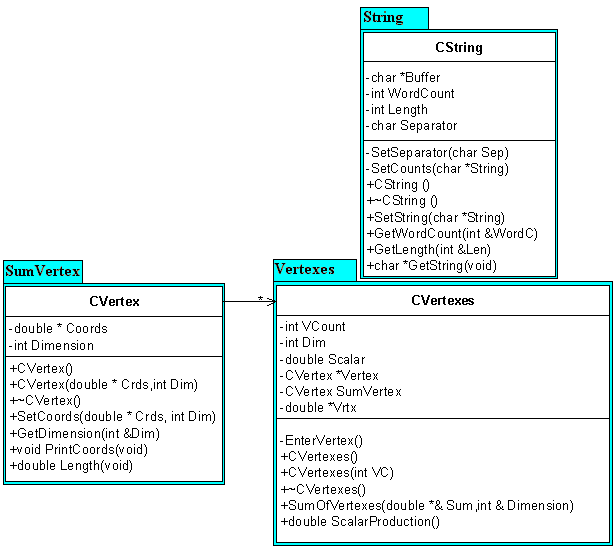
Orai03-1.Cpp, Orai03-2.Cpp
3-4. Gyakorlat (házi feladat) (1):Langrange interpoláció:
adottak xi (i=0,1,..,n) alappontok, yi (i=0,1,..,n) függvényértékek,
n az alappontok száma -1. Keresendő egy olyan g függvény melyre yi=g(xi).
Tegyük fel, hogy g(x) legfeljebb n-ed fokú polinom. Ekkor g felírható: g(x)=c0+c1x+c2x2+..+cnxn.
(Bizonyítható, hogy egyértelműen található ilyen legfeljebb n-ed fokú
polinom, adott xi,yi esetén.). Az együtthatók megtalálását
két lépésben végezzük.
Először meghatározzuk, az un. Newton együtthatókat:
ai (i=0,1,..,n), ahol g(x)=a0+a1*(x-x0)+a2*(x-x0)*(x-x1)+a3*(x-x0)*(x-x1)*(x-x2)+..+an*(x-x0)*..*(x-xn-1)
Az
algoritmus formális leírása: Harung Ferenc Bevezetés a Numerikus Analízisbe
c. könyve alapján (185. oldal)
INPUT: n-az alappontok száma-1
xi (i=0,1,..,n) alappontok
yi (i=0,1,..,n) függvényértékek
OUTPUT: ai (i=0,1,..,n) Newton polinom együtthatói.
for
i=0,1,..,n do
ai¬yi
end do
for j=1,2,..,n do
for i=n,n-1,..,j do
ai¬(ai-ai-1)/(xi-xi-j)
end do
end do
output (a0,a1,..,an,)
Newton polinom
kiértékelése:
INPUT: n-az alappontok száma-1
ai (i=0,1,..,n) Newton polinom együtthatói
yi (i=0,1,..,n) függvényértékek
x - a pont ahol kiértékeljük a polinomot
OUTPUT: y a Newton polinom értéke x-ben.
y¬an
for i=n-1,n-2,..,0 do
y¬y*(x-xi)+ai
end do
output y
A Newton polinom együtthatóiból ck (k=0,1,...,n)
már könnyen számítható.
pl.
Ekkor a Newton polinom együtthatói ai= -2 1 -1 1. Ebből g(x)=-2+1*(x+1)-1*(x+1)*(x-1)+1*(x+1)*(x-1)*(x-2)
= x3-3x2+2
3-4. Gyakorlat (házi feladat) (2): Bezier
görbék, Bernstein együtthatók segítségével.
Definíció: Legyen az i-edik n-ed rendű Bernstein polinom a következő:
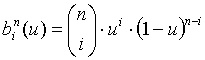 ,
ahol
,
ahol 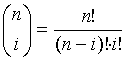 ,
, 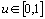 .
.
Példa: 4 pont által meghatározott Bezier görbe.
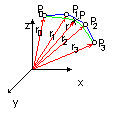 A
Bernstein együtthetók ebben az esetben:
A
Bernstein együtthetók ebben az esetben:
b03(u)=(1-u)3
b13(u)=3u*(1-u)2
b23(u)=3u2*(1-u)
b33(u)=u3
Ebből P pont koordinátája: P=r(u)=b03(u)*r0+b13(u)*r1+b23(u)*r2+b33(u)*r3
Tehát pl. ez a görbe a térben:
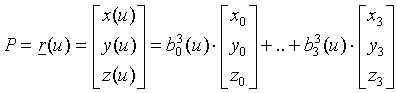 . Általánosságban
egy n csúcshoz tartozó Bezier görbén lévő pont egyenlete:
. Általánosságban
egy n csúcshoz tartozó Bezier görbén lévő pont egyenlete:
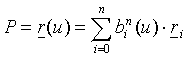
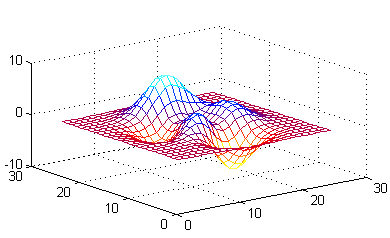 Felület
esetén a Bezier felületet szintén ki lehet számolni az alábbi összeföggés
alapján:
Felület
esetén a Bezier felületet szintén ki lehet számolni az alábbi összeföggés
alapján:
Egy pont a Bezier felületen::
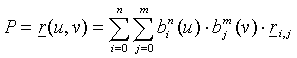 ,
ahol
,
ahol 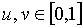
5.
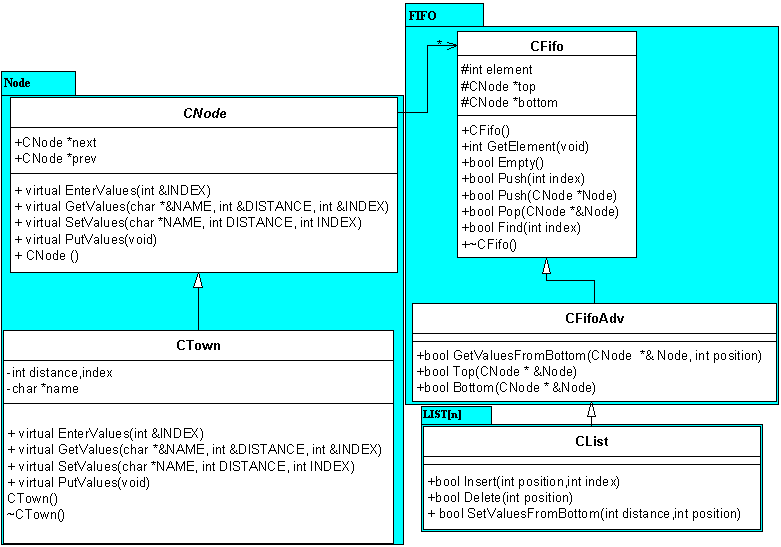
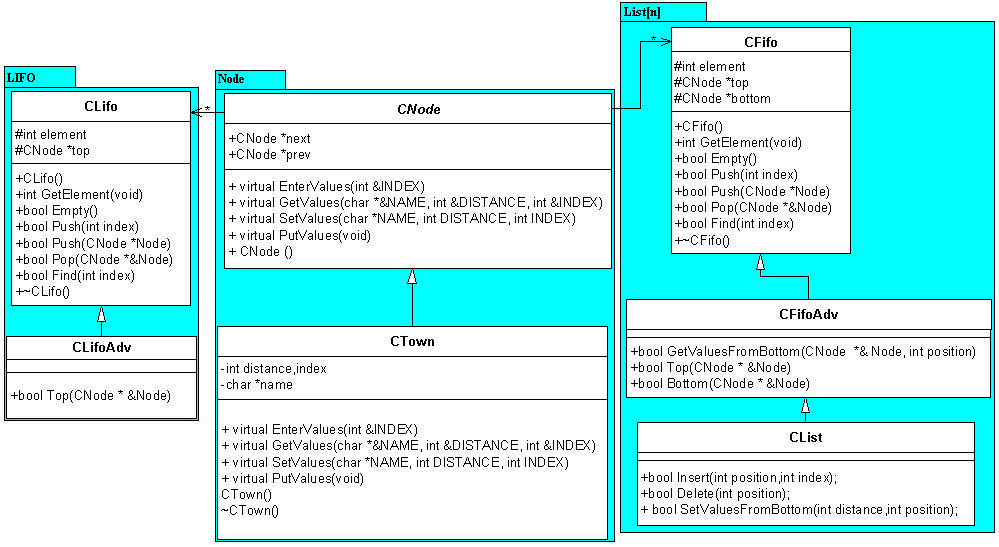
Gyakorlat: Feladatok osztályokkal II – FIFO megvalósítása,
öröklődés
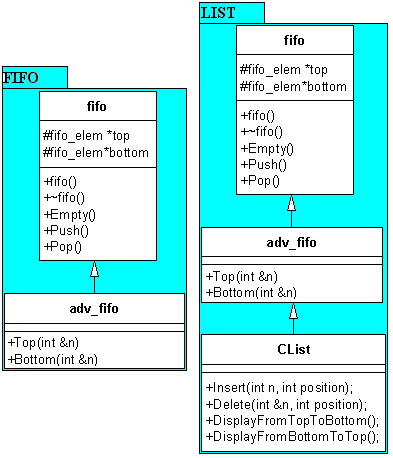
1., Készítsen
olyan osztály, mely egy dinamikusan lefoglalt FIFO tárat valósít meg kétirányú
láncolt lista segítségével! Származtasson le az ős osztályból egy újabb
adv_fifo osztályt, amely rendelkezik, Top és Bottom tagfüggvényekkel is.
2., Származtasson
le az adv_fifo osztályból, CList osztályt, mely egy kétirányú láncolt
listát valósít meg. A láncolt listába, lehessen egy tetszőleges pozícióba
új elemet beszúrni. Lehessen tetszőleges pozícióból elemet törölni.
Legyen olyan tagfüggvénye, amely a top/bottom mutatótól kezdve kiírja az
elemeket.
Orai05-1.Cpp, Orai05-2.Cpp
5. Gyakorlat (házi feladat): Nelder – Mead korlátos
szélsőérték-kereső algoritmus.
A feladat:
gi(x)≥0, i=1,2,..,m
max f
Előzetes feltételek:
a., a D halmaz konvex
b., ismerjük a halmaz egy belső
pontját
Kiinduló szimplex konstruálása:
-
xo az ismert belső pont
-
xi:=xo+Diei i=1,2,..,n
-
pontok (ei az i. egységvektor)
olyan szimplex csúcsai, amelynek minden pontja a D-nek belső pontja. Az
aktuális Di megválasztása próbálgatással történhet.
Az iterációs szabályt a blokkvázlatból lehet
kiolvasni:
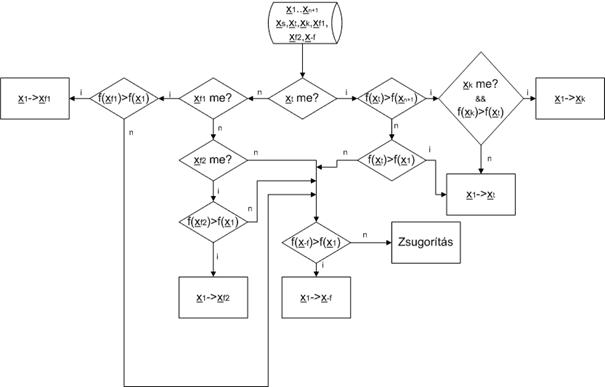
A blokkvázlat
szereplői:
x1: a szimplex azon pontja, melyben f
érteke a legkisebb
xn+1: a szimplex azon pontja, melyben f
érteke a legnagyobb
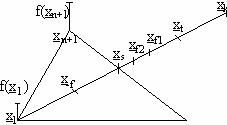
xs: az x2, x3,..,xn+1
pontok súlypontja
xt: x1 tükörképe xs-re
vonatkozóan
xk: olyan pont, hogy xt felezi
xs és xk távolságát
xf1: az xs xt
szakasz felezőpontja
xf2: az xs xf1
szakasz felezőpontja
x-f: az x1 xs
szakasz felezőpontja
Számítások:
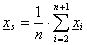 ,
,
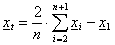 ,
, 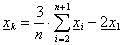 ,
, 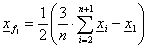 ,
,
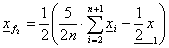 ,
, 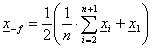
A zsugorítás xn+1
körüli ½ -es kicsinyítést jelent. Számítása:
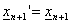 ,
,
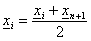
Az algoritmus
megáll, ha:
1.
Elértünk egy megadott iterációs számot vagy
2.
A tapasztalati szórás s*<e
A tapasztalati szórás számítása: 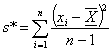
6.
Gyakorlat: Feladatok osztályokkal III
– Lista megvalósítása, öröklődés, virtuális függvények
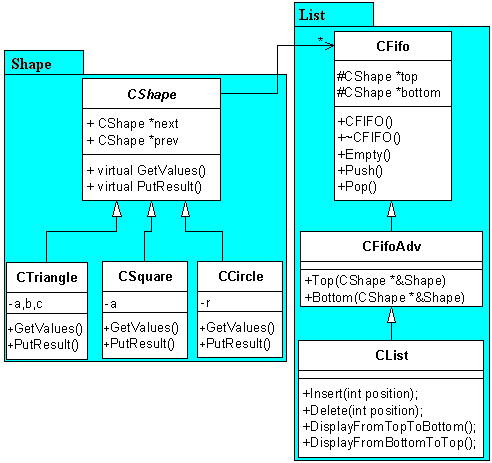
Orai06.Cpp
6. Gyakorlat (házi feladatok):
Feladatok osztályokkal IV - Gráfelméleti algoritmusok

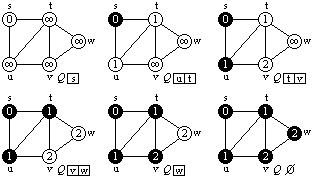
BFS (Breadth First Search) algoritmus
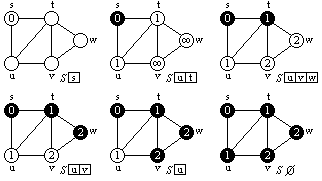
DFS (Depth First Search) algoritmus
7.
Gyakorlat: Feladatok osztályokkal IV
– Bináris fák
Készítsen olyan osztályt, mely
egy adott számú (tetszőleges típusú) elemet tart nyílván. Rendezze az
elemeket a HeapSort algoritmus segítségével.
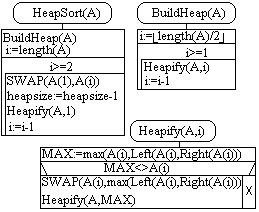
Orai07.Cpp, Orai07.H
7. Gyakorlat (házi feladatok): Feladatok osztályokkal
IV - Gráfelméleti algoritmusok II
Kruskal, Prim, Sollin algoritmus megvalósítása kétirányú láncolt listával.
Kruskal algoritmus:
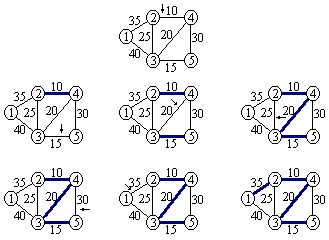
Prim algoritmus:
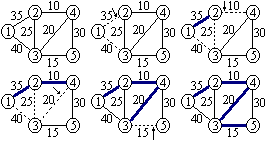
algorithm heap-Prim;
begin
create-heap(H);
for
each jÎN-{1}
do d(j):=C+1;
set d(1):=0; and pred(1):=0;
for each jÎN-{1}
do insert(j,H);
T*:=0;
while |T*|<(n-1) do
begin
find-min(I,H);
delete-min(i,H);
T*:=T*E(pred(i),i);
for each (i,j)ÎA(i)
with jÎH
do
if d(j)>cij
then
begin
d(j):=cij;
pred(j):=i;
decrease-key(j,cij,H);
end;
end;
end;
T* is a minimum spanning tree
end;
Sollin algoritmus:
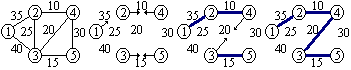
algorithm Sollin;
begin
for each iÎN
do Ni:={i};
T*:=A;
while |T*|<(n-1) do
begin
for each tree Nk do
nearest-neighbour(Nk,ik,jk);
for each tree Nk do
if nodes ik and jk belong
to different trees then
merge (ik,jk) and update T*:=T*E{(ik,jk)};
end;
end;
8.
Gyakorlat: Feladatok osztályokkal V – Operátorok túlterhelése
Készítsen olyan osztályt, mely egy halmaz elemeit
tartalmazza. Értelmezze az osztályon két (vagy több) halmaz unióját (+), különbségét
(-), metszetét (*) az operátorok túlterhelésének segítségével.
Majd készítsen olyan osztályt amely egy vektor adatai tartja nyilván és értelmezze
rajta a +,-,* műveleteket!
Orai08-1.Cpp, Orai08-2.Cpp
8. Gyakorlat (házi feladat): Feladatok osztályokkal V -
Gráfelméleti algoritmusok III
Dijkstra algoritmus megvalósítása kétirányú láncolt listával.
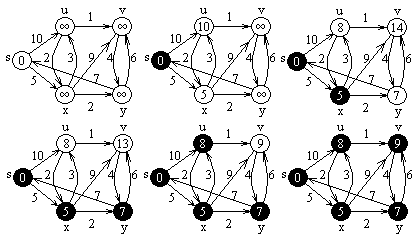
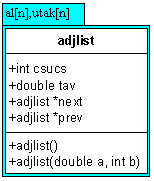
9.
Gyakorlat: Feladatok osztályokkal VI
– Operátorok túlterhelése
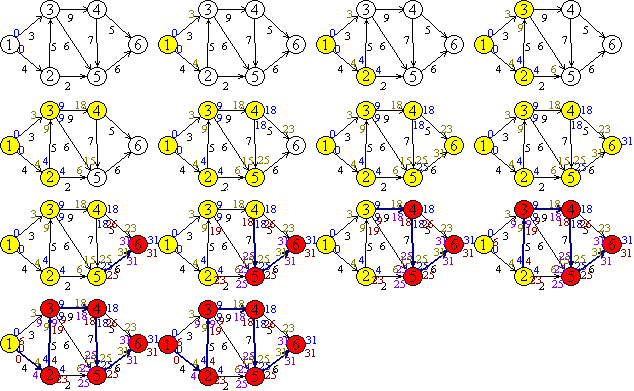
Tevékenységlista
| Tevékenységek |
Lefutási idő |
Legkorábbi
kezdés |
Legkorábbi
befejezés |
Legkésőbbi
kezdés |
Legkésőbbi
befejezés |
| (i,j) |
d(i,j) |
EST(i,j) |
EFT(i,j) |
LST(i,j) |
LFT(i,j) |
| (1,2) |
4 |
0 |
4 |
0 |
4 |
| (1,3) |
3 |
0 |
3 |
6 |
9 |
| (2,3) |
5 |
4 |
9 |
4 |
9 |
| (2,5) |
2 |
4 |
6 |
23 |
25 |
| (3,4) |
9 |
9 |
18 |
9 |
18 |
| (3,5) |
6 |
9 |
15 |
19 |
25 |
| (4,5) |
7 |
18 |
25 |
18 |
25 |
| (4,6) |
5 |
18 |
23 |
26 |
31 |
| (5,6) |
6 |
25 |
31 |
25 |
31 |
Eseménylista
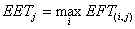 ,
,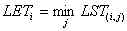
| Események |
Legkorábbi
bekövetkezés |
Legkésőbbi
bekövetkezés |
| 1 |
0 |
0 |
| 2 |
4 |
4 |
| 3 |
9 |
9 |
| 4 |
18 |
18 |
| 5 |
25 |
25 |
| 6 |
31 |
31 |
Kritikus út: 1-2-3-4-5-6
A kritikus út hossza: 31
CPM-Hálótervezés -
fogalmak, feladatok, megoldások
10.
Gyakorlat: Feladatok osztályokkal VII, template-ek I
Készítsen olyan osztályt, mely egy adott számú
(tetszőleges típusú) elemet tart nyílván. Rendezze az elemeket a HeapSort
algoritmus segítségével.
Orai10.Cpp, Orai10.H
10. Gyakorlat (házi feladat): Feladatok osztályokkal
VIII - Gráfelméleti algoritmusok
Tartalékidők számítása:
1., Tevékenység tartalékidők
a., teljes tartalékidő = LST(i,j)-EST(i,j)=LFT(i,j)-EFT(i,j)
b., szabad tartalékidő = EETj-EETi-d(i,j)
c., feltételes tartalékidő = teljes tartalékidő - szabad
tartalékidő
d., független tartalékidő = EETj-LETi-d(i,j)
2., Esemény tartalékidő = LETi-EETj
11. Gyakorlat:
Feladatok osztályokkal VIII – template-ek
II
Készítsen
olyan osztályt, mely egy adott számú (tetszőleges típusú) elemet tart nyílván.
Rendezze az elemeket a QuickSort algoritmus segítségével.
Orai11.Cpp, Orai11.H
Feladatok osztályokkal X - Gráfelméleti
algoritmusok
Valósítsa meg a CPM/COST algoritmust
| Tevékenység |
dni,j |
dri,j |
Cn |
- Ci,j |
| (1,2) |
7 |
5 |
1 500 |
100 |
| (1,3) |
5 |
4 |
1 600 |
400 |
| (1,4) |
10 |
6 |
2 200 |
150 |
| (2,4) |
6 |
3 |
1 800 |
50 |
| (3,4) |
6 |
5 |
1 400 |
180 |
| (4,5) |
9 |
7 |
2 000 |
300 |
| Összesen: |
10 500 |
- |
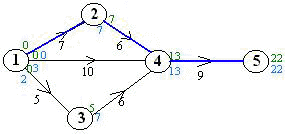
A kritikus út hossza: 22
A kritikus út elemei: 1-2-4-5
| Lépések száma |
Csökkentett tevékenységek jelei |
Csökkentés mértéke |
Költségnövekedési tényező |
Költségnövekedés |
Összes költség |
Kritikus út hossza |
| 0 |
- |
- |
- |
- |
10 500 |
22 |
| 1 |
(2,4) |
2 |
50 |
100 |
10 600 |
20 |
| 2 |
(2,4) és (3,4) |
1 |
230 |
230 |
10 830 |
19 |
| 3 |
(4,5) |
2 |
300 |
600 |
11 430 |
17 |
| 4 |
(1,2) és (1,3) és (1,4) |
1 |
650 |
650 |
12 080 |
16 |
12. Gyakorlat:
Feladatok osztályokkal IX
Valósítsa meg a BucketSort algoritmust
i=1,2,..,n, 0<=A[i]<=1
B[0..n-1]
procedure Bucket_sort(A)
begin
n:=length(A);
for i:=1 to n do
insert A[i] into list B[ënA[i]û];
for i:=1 to n-1 do sort B[i]
with insertion_sort;
concate B[0]..B[n-1];
end;
Példa:
GYAK.Exe, HF.Exe
További letölthető file-ok
Beadandó feladatok:
Bead.Doc
Beadott prezentációk:
Alapértelmezett, és paraméterezett
konstruktorok
Sablonok
Segítség a beadandó feladatokhoz:
Calc.Cpp, Calc.Doc,
Beker.Cpp
Kapcsolódó oldalak:
2001-es
gyakorlatokon tárgyalt feladatok
Bertók Botond oktatási segédanyagai
Bertók Botond hivatalos honlapja (angol)
Számítástudomány Alkalmazása Tanszék (angol)
Veszprémi Egyetem
A honlapot készítette Kosztyán
Zsolt Tibor
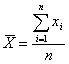 .
.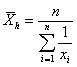
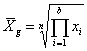
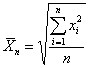
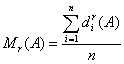 , ahol
, ahol
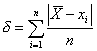
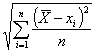


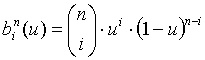
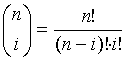 ,
,  A
Bernstein együtthetók ebben az esetben:
A
Bernstein együtthetók ebben az esetben: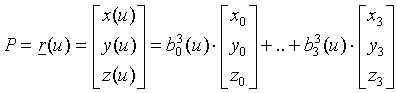 . Általánosságban
egy n csúcshoz tartozó Bezier görbén lévő pont egyenlete:
. Általánosságban
egy n csúcshoz tartozó Bezier görbén lévő pont egyenlete: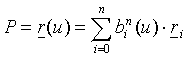
 Felület
esetén a Bezier felületet szintén ki lehet számolni az alábbi összeföggés
alapján:
Felület
esetén a Bezier felületet szintén ki lehet számolni az alábbi összeföggés
alapján: 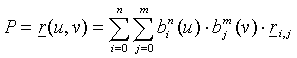 ,
ahol
,
ahol 


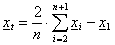 ,
, 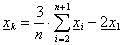 ,
, 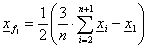 ,
,
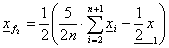 ,
,