Hamilton körök, síkba teríthetőség

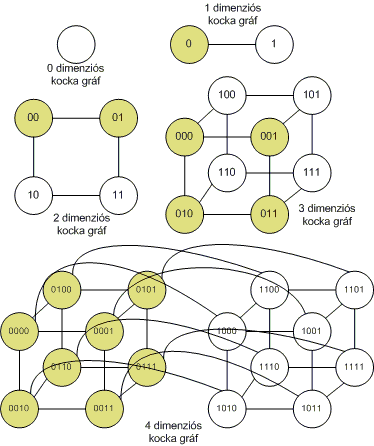
Tekintsük az n dimenziós kocka-gráfot, melynek képzése a következő: 0 dimenziós kockagráf legyen egy izolált pont. n dimenziós kockagráfból úgy képezünk n+1 dimenzós kocka gráfot, hogy lemásoljuk az eredeti gráfot, ezután az azonos jelzetü csúcsokat összekötjük. Az eredeti gráf csúcsainak számai elé 0-át, a másolat csúcsainak számai elé 1-et írunk. Ekkor n dimenziós kocka gráf esetén a csúcsok számozása egy n hosszúságú bináris szám lesz. Tekintsük továbbiakban az n>=1 esetet. Hány dimenzós kockagráf teríthető még síkba? (+4p). Találjon olyan polinomiális módszert, amely egy n dimenziós gráfban keres olyan Hamilton kört, melynél a csúcsok számai csak egy helyiértékben térnek el egymástól (ezek az un. Gray kódok pl. n=2 esetén 00,01,11,10,00) (+20p). Tegyük fel, hogy mindíg az azonosan nulla csúcsból indulunk. Létezik-e minden n>=1-re ilyen Hamilton kör? (illetve ennek megfelelő Gray kód?) (+10p). Egyértelmű-e a megoldás? (+6p)