Zárthelyi feladatok, és megoldásaik

1. Zárthelyi feladat: 2001.02.13 12.00 óra

A csoport: Valós (típusú) tömbben a nemnegatív elemek átlagának meghatározása. (Amennyiben nincs nemnegatív elem a tömbben, akkor 0-t adjon vissza a függvény. Megoldásra szánt idő: 2 perc)

B csoport: Egész (típusú) tömbben abszolút értékben legkisebb érték meghatározása. (Megoldásra szánt idő: 1 perc)

2. Zárthelyi feladat: 2001.02.20 12.00 óra

A csoport: Rendezzen csökkenő sorrendben egy valós tömböt a maximum kiválasztás módszerével. Írja le a csere (Replace) függvényt is. (Megoldásra szánt idő: 3 perc.)

B csoport: Rendezzen csökkenő sorrendben egy egész típusú tömböt a buborékrendezés módszerével. Írja le a csere (Replace) függvényt is. (Megoldásra szánt idő: 2 perc.)

3. Zárthelyi feladat: 2001.02.27 12.00 óra

A csoport: Rendezzen növekvő sorrendben egy egész (típusú) tömböt a maximum kiválasztás módszerével. (Megoldásra szánt idő: 3 perc.)

B csoport: Adott intervallumba eső valós szám bekérése. (Megoldásra szánt idő: 2 perc.)

4. Zárthelyi feladat: 2001.03.06 12.00 óra

A csoport: Kérje be egy adott intervallumba eső valós tömb értékeit. Írja le a teljes programot. (Megoldásra szánt idő: 8 perc.)

B csoport: Verem megvalósítása dinamikusan láncolt kétirányú listával. (Megoldásra szánt idő: 7 perc.)

5. Zárthelyi feladat: 2001.03.20 12.00 óra

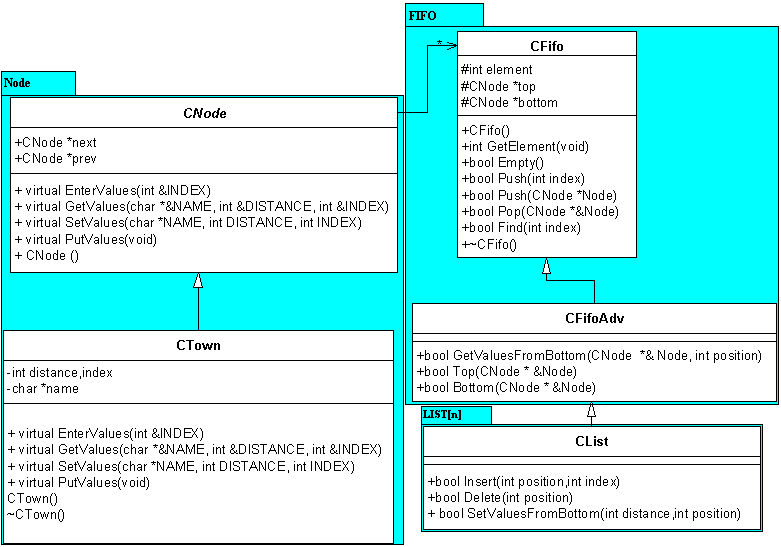
A csoport: FIFO megvalósítása dinamikusan láncolt kétirányú listával. (Megoldásra szánt idő: 15 perc.)

B csoport: Veremmeg valósítása kétirányú láncolt listával. Származtasson le a stack ősosztályból egy származtatott osztályt, mely rendelkezik egy olyan Top függvénnyel, ami visszaadja a stack tetején lévő elemet. (Megoldásra szánt idő: 14 perc.)

6. Zárthelyi feladat: 2001.03.27 12.00 óra

A csoport: Valós tömb elemeinek szórásának meghatározása. (Megoldásra szánt idő: 2 perc.)

B csoport: Írjon olyan függvényt, mely egy valós tömb második legnagyobb elemét adja vissza. (Megoldásra szánt idő: 3 perc.)

7. Zárthelyi feladat: 2001.04.03 12.00 óra

A csoport:    Kétféle területszámoló eljárás azonos őssel és módósított virtuális metódussal. Az egyik metódus egy kör, még a másik egy négyzet területét számítja ki. Írja le a teljes programot. Megoldásra szánt idő: 16 perc.)

B csoport:    Rendezzen növekvő sorrendben egy egész (típusú) tömböt a maximum kiválasztás módszerével. Írja le a teljes programot. Megoldásra szánt idő: 15 perc.)

8. Zárthelyi feladat: 2001.04.17 12.00 óra

A csoport: Rendezzen növekvő sorrendbe egy valós tömböt a bináris keresőfa segítségével. Írja le a teljes programot. (Megoldásra szánt idő: 16 perc.)

B csoport: FIFO megvalósítása dinamikusan láncolt kétirányú listával. (Megoldásra szánt idő: 15 perc.)

9. Zárthelyi feladat: 2001.04.24 12.00 óra

A csoport: Készítse el a string osztály == összehasonlító operátorát. (Megoldásra szánt idő: 3 perc.)

B csoport: Valós (típusú) tömbben a negatív elemek átlagának meghatározása. (Amennyiben nincs negatív elem a tömbben, akkor 0-t adjon vissza a függvény. Megoldásra szánt idő: 2 perc)

10. Zárthelyi feladat: 2001.05.08 12.00 óra

A csoport: Készítse el a string osztály <= összehasonlító operátorát. (Megoldásra szánt idő: 4 perc.)

B csoport: Készítsen olyan füügvényt, amely természetes számokat tartalmazó egész típusú tömb legnagyobb páros elemét adja vissza. Ha nincs ilyen elem, akkor térjen vissza -1-el. (Megoldásra szánt idő: 3 perc)

Összes eddigi zárthelyi feladat megoldása:

ZH.Exe

Gyakorlati órákon tárgyalt feladatok, és megoldásaik

1. Gyakorlat: A C++ nyelvi elemeinek gyakorlása feladatokkal.

1. Valós (dinamikusan lefoglalt) tömb adatainak bekérése, összeg/átlag meghatározása.
2. Szóródási mutatók meghatározása:
   a.) Terjedelem:
   b.) Átlagos eltérés:
   c.) Variancia:
   d.) Szórás:
   e.) Realtív szórás:

2. Gyakorlat: A C++ nyelvi elemeinek gyakorlása feladatokkal. II

1. Egész típusú (dinamikusan lefoglalt) tömb véletlen adatokkal való feltöltése, átmásolása egy másik tömbbe. A tömbök rendezése minimum-kiválasztásos, és buborékrendezés segítségével. A futásidők összehasonlítása.
2. A cos(x²) a és b közötti határozott integráljának meghatározása az alábbi numerikus integrál közelítő módszerekkel. Készítsen olyan függvényt, amely fokból radiánba, radiánból fokba számít.
   • Téglalap formula: h(y₀+y₁+y₂+..+y_n-1), vagy h(y₁+y₂+..+y_n-1+y_n)
   • Trapéz formula: h(y₀/2+ y₁+y₂+..+y_n-1+ y_n/2)
   • Simpson formula: h(y₀+ 4y₁+2y₂+4y₃+..+2y_n-2+4y_n-1+ y_n)/3 (ha n=2k)

3. Gyakorlat: Feladatok osztályokkal.

1. Készítse el a következő osztálydefiníciót, és hozza létre az osztály egy statikus példányát.
   • Osztály neve:

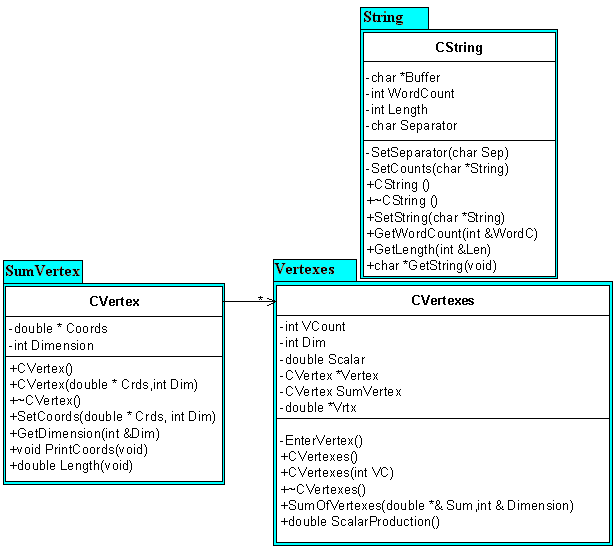
   CString;

   Adattagok:

   Buffer //Ez tartalmazza a stringet.
   WordCount //A stringben szereplő szavak számát tartalmazza.
   Length //A string hosszát tartalmazza.
   Fügvénytagok: (saját függvények)
   SetSeparator //Az elválasztó jelet állítja be.
   SetCount //A szavak számát állítja be.
   (nyilvános függvények)
   SetString //Új stringet definiál.
   GetString //Visszaadja a jelenleg tárolt stringet.
   GetWordCount //A szavak számát adja vissza.
   GetLength //A string hosszát adja vissza.
   Készítsen két konstruktort. Egy alapértelmezettet, mely a Buffer-nek egy üres stringet ad át, és egy olyat, melynek át lehet adni egy stringet, valamint készítsen destruktort is.
   

2. Készítsen egy CVertex osztályt, mely tartalmazza, a valós típusú vektort, a szükséges bekérő, módosító, lekérdező függvényeket. Készítsen olyan CVertexes objektumot, melynek VCount db. vektortagja van, tartalmazza az osztály olyan függvényt, mely visszaadja a vektorok összegét, és skaláris szorzatát.

4. Gyakorlat: Feladatok osztályokkal II - FIFO megvalósítása, öröklődés

1. Készítsen olyan osztály, mely egy dinamikusan lefoglalt FIFO tárat valósít meg kétirányú láncolt lista segítségével! Származtasson le az ős osztályból egy újabb adv_fifo osztályt, amely rendelkezik, Top és Bottom tagfüggvényekkel is.
2. Származtasson le az adv_fifo osztályból, CList osztályt, mely egy kétirányú láncolt listát valósít meg. A láncolt listába, lehessen egy tetszőleges pozícióba új elemet beszúrni. Lehessen tetszőleges pozícióból elemet törölni. Legyen olyan tagfüggvénye, amely a top/bottom mutatótól kezdve kiírja az elemeket.

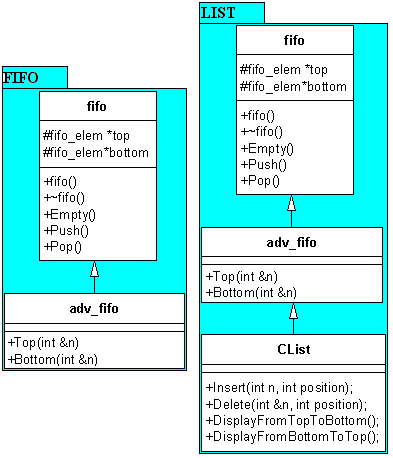
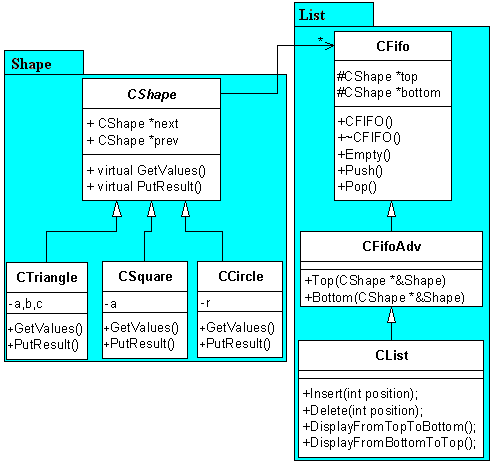
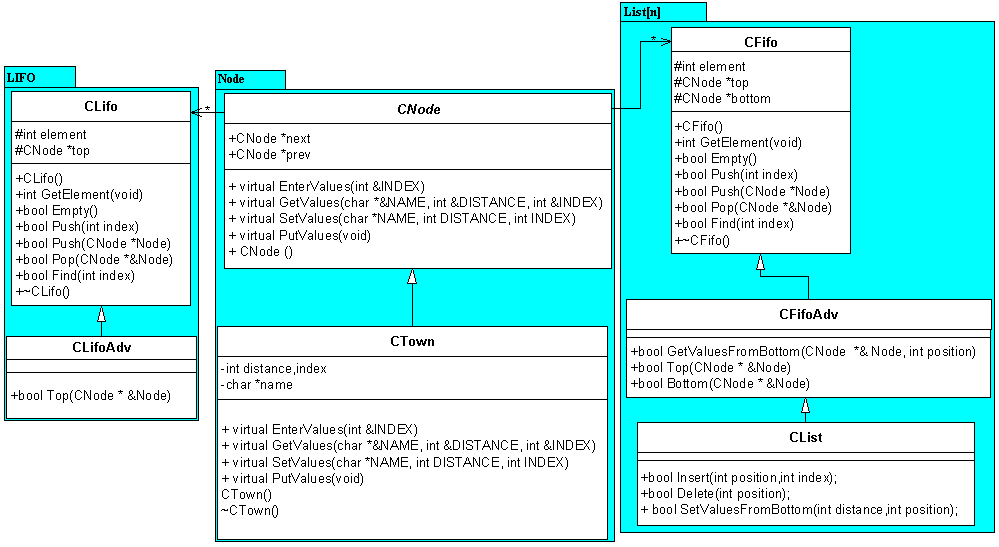
5. Gyakorlat: Feladatok osztályokkal III - Lista megvalósítása, öröklődés, virtuális függvények

Készítsen olyan listát, mely adott alakzatoknak (háromszög, négyszög, kör) az adatait tárolja, valamint kiszámolja az egyes alakzatok területét, és kerületét.

6. Gyakorlat: Feladatok osztályokkal IV - Operátorok túlterhelése

Készítsen olyan osztályt, mely egy mátrix adatait tartja nyilván. Értelmezze az osztályon két (vagy több) mátrix összeadását, kivonását, szorzását az operátorok túlterhelésének segítségével.

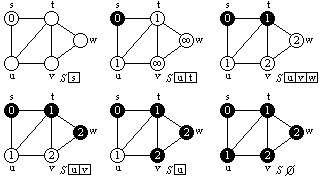
6. Gyakorlat (házi feladatok): Feladatok osztályokkal IV - Gráfelméleti algoritmusok

BFS (Breadth First Search) algoritmus

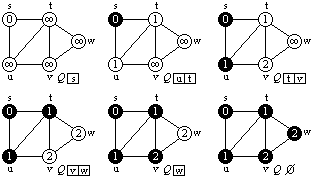
DFS (Depth First Search) algoritmus

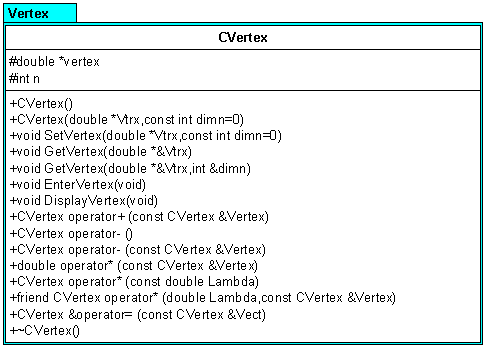
7.  Gyakorlat: Feladatok osztályokkal V - Operátorok túlterhelése II

Készítsen olyan osztályt, mely egy vektor adatait tartja nyilván. Értelmezze az osztályon két (vagy több) vektor összeadását, kivonását, skaláris szorzását az operátorok túlterhelésének segítségével.

7. Gyakorlat (házi feladat): Feladatok osztályokkal V - Gráfelméleti algoritmusok
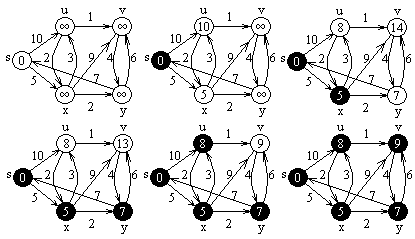
Dijkstra algoritmus megvalósítása kétirányú láncolt listával.

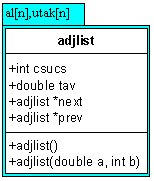
8. Gyakorlat: Feladatok osztályokkal VI - Bináris fák, template-ek

Készítsen olyan osztályt, mely egy adott számú (tetszőleges típusú) elemet tart nyílván. Rendezze az elemeket a HeapSort algoritmus segítségével.

Egy tömb elemeinek reprezentálása bináris fában:   4
                                                                            /    \
index: 1,2,3,4,5,6,7, 8,  9, 10                             1     2
érték: 4,1,2,7,8,9,3,10,14,16                            /   \   /  \
                                                                       7    8 9  3
Heap tulajdonság:                                        /   \  /
Key(Parent(x))<=Key(x) (x<>Root)           10 14 16

Tömbben egy i indexü elem gyermekei Left(i):=2*i, Right(i):=2*i+1

A HeapSort algoritmusvázlata:

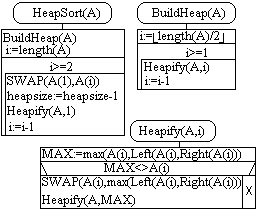
8. Gyakorlat (házi feladatok): Feladatok osztályokkal VI - Gráfelméleti algoritmusok
Kruskal, Prim, Sollin algoritmus megvalósítása kétirányú láncolt listával.

Kruskal algoritmus:

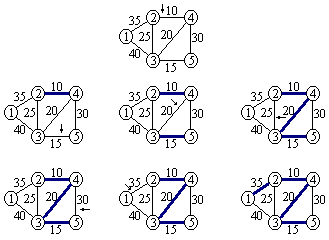
Prim algoritmus:

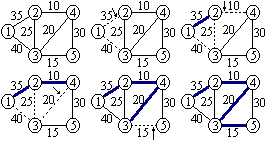
algorithm heap-Prim;
begin
create-heap(H);
        for each jÎN-{1} do d(j):=C+1;
set d(1):=0; and pred(1):=0;
for each jÎN-{1} do insert(j,H);
T*:=0;
while |T*|<(n-1) do
begin
        find-min(I,H);
        delete-min(i,H);
        T*:=T*E(pred(i),i);
        for each (i,j)ÎA(i) with jÎH do
            if d(j)>cij then
            begin
                    d(j):=cij;
                    pred(j):=i;
                    decrease-key(j,cij,H);
            end;
    end;
end;
T* is a minimum spanning tree
end;

Sollin algoritmus:

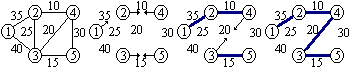
algorithm Sollin;
begin
        for each iÎN do Ni:={i};
        T*:=A;
        while |T*|<(n-1) do
        begin
        for each tree Nk do nearest-neighbour(Nk,ik,jk);
        for each tree Nk do
            if nodes ik and jk belong to different trees then
                merge (ik,jk) and update T*:=T*E{(ik,jk)};
end;
end;

9. Gyakorlat: Feladatok osztályokkal VII - Operátorok felültöltése III

Készítsen olyan osztályt, mely egy halmaz elemeit tartalmazza. Értelmezze az osztályon két (vagy több) halmaz unióját (+), különbségét (-), metszetét (*) az operátorok túlterhelésének segítségével.

9. Gyakorlat (házi feladat): Feladatok osztályokkal VII - Gráfelméleti algoritmusok
CPM (Critical Path Method) algoritmus megvalósítása kétirányú láncolt listával.

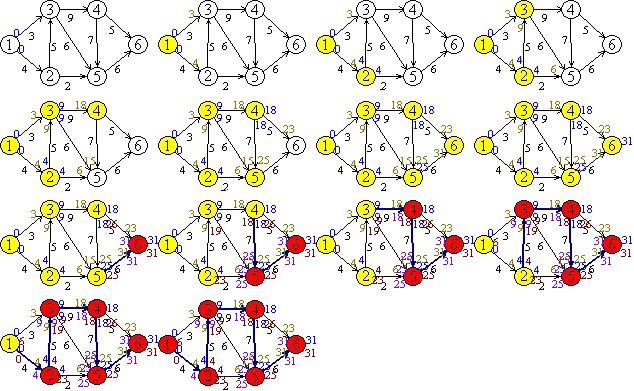
Tevékenységlista

Eseménylista

Kritikus út: 1-2-3-4-5-6
A kritikus út hossza: 31

CPM-Hálótervezés - fogalmak, feladatok, megoldások

10. Gyakorlat: Feladatok osztályokkal VIII - operátor felültöltés IV, template-ek II

1. Egészítse ki az (órán tanult) string osztályt az összehasonlító operátorok felüldefiniálásával.

2. Készítsen olyan osztályt, mely egy adott számú (tetszőleges típusú) elemet tart nyílván. Rendezze az elemeket a QuickSort algoritmus segítségével.

procedure quicksort(p,q)
begin
        i=p,j=q,k=Buffer[((p+q) div 2)];
        repeat
                while (Buffer[i]<k) do i:=i+1;
                while (k<Buffer[j]) do j:=j-1;
                if (i<=j) then
                begin
                        Swap(i,j);
                        i:=i+1;
                        j:=j-1;
                end;
        until (i>j);
        if (p<j) then quicksort(p,j);
        if (i<q) then quicksort(i,q);
end;

10. Gyakorlat (házi feladat): Feladatok osztályokkal VIII - Gráfelméleti algoritmusok

Tartalékidők számítása:

1., Tevékenység tartalékidők

a., teljes tartalékidő = LST(i,j)-EST(i,j)=LFT(i,j)-EFT(i,j)

b., szabad tartalékidő = EETj-EETi-d(i,j)

c., feltételes tartalékidő = teljes tartalékidő - szabad tartalékidő

d., független tartalékidő = EETj-LETi-d(i,j)

2., Esemény tartalékidő = LETi-EETj

11. Gyakorlat: Feladatok osztályokkal IX - operátor felültöltés V

Egészítse ki az (órán tanult) string osztályt a [], >> operátorok felüldefiniálásával. Valósítsa meg a Boyer Moore stringkeresési algoritmust.

12. Gyakorlat: Feladatok osztályokkal X

Valósítsa meg a BucketSort algoritmust

i=1,2,..,n, 0<=A[i]<=1
B[0..n-1]

procedure Bucket_sort(A)
begin
n:=length(A);
for i:=1 to n do
    insert A[i] into list B[ënA[i]u];
for i:=1 to n-1 do sort B[i] with insertion_sort;
concate B[0]..B[n-1];
end;

Példa:

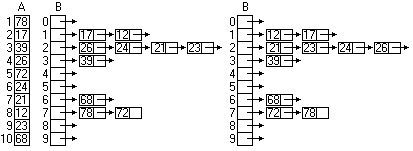
12. Gyakorlat (házi feladat): Feladatok osztályokkal X - Gráfelméleti algoritmusok

Valósítsa meg a CPM/COST algoritmust

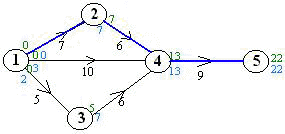
A kritikus út hossza: 22
A kritikus út elemei: 1-2-4-5

További letölthető file-ok

Beadandó feladatok:

Bead.Doc

Segítség a beadandó feladatokhoz.

Calc.Cpp, Calc.Doc, Beker.Cpp

Kapcsolódó oldalak:

A honlapot készítette Kosztyán Zsolt Tibor